The last we spoke about asynchronous programming, I paused with the notion of thinking about distributed systems as data pipelines. Let’s dig a little deeper into this, and talk about the concepts of throughput, capacity, and backpressure in building resilient systems.
We have seen how asynchronous programs “stash-away” uncompleted tasks till they are notified by someone of their completion. This can be interpreted as building a “queue” of unfinished tasks between the asynchronous caller and callee. In fact, if we are using thread-pools for asynchronous programming, we have to explicitly use a queue to transfer tasks and then wait for result. In event-based systems the same interpretation can be made by thinking that having invoked the caller and waiting for result is no different from queueing a task and waiting for completion.
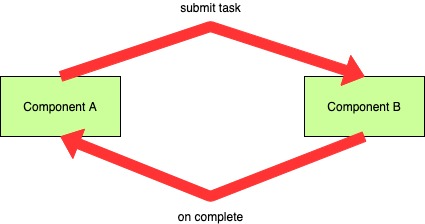
This is very similar to message-based communication between two independent systems (over a message broker like Kafka or RabbitMQ). A system invokes a remote system/method asynchronously and awaits the completion of the invocation. The waiting terminates when a completion signal/message is received.
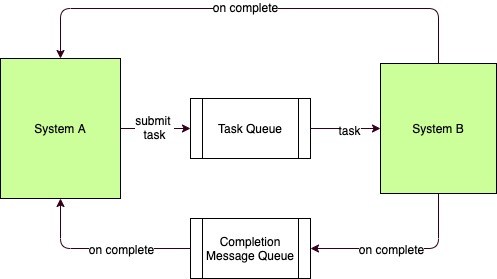
Theoretically, there is no difference between the two models. And the common element between the micro and macro scenarios is the concept of the queue. Both use queues as buffers to temporally isolate the caller from the callee.
So all distributed systems, when visualized end-to-end, are stream processing systems, regardless of their implementation details. Asynchronous systems, distributed or not, can ALWAYS be interpreted as stream processing systems (since a handover-interrupt model is built into them). With this in mind, we can now start applying queueing theory to how we look at scaling software systems.
Throughput and Capacity
If we have a hose with water being pumped in from one side and used at the other, what would we do to push as much water through as possible?
The first thing is to make sure that water goes out of the hose as fast as possible. This can be achieved by making the consuming side of the hose as frictionless as possible. Remove all obstructions, make it fast to get water out. If all the water being pushed in can be taken out at the exact same rate, then there is no “bottleneck” and we can push more and more water. In software terms, this is the equivalent of increasing throughput, i.e., taking less time per unit work. When we think of reducing response times or using faster algorithms, we are thinking in terms of throughput. Throughput is usually measured in time-per-request, Teams spend a LOT of time and effort in this type of optimization, writing better code, smarter algorithms, adding caches, etc.
Let’s say a user invokes system A that needs to invoke system B to do its job. Let’s assume both A and B are single-threaded and synchronously programmed. The user wants to call system A as often as possible. But due to its synchronous and single-threaded nature, A can only accept one request at a time. So we cannot add any more users, and the only way to get more out of the system is to make both A and B very very fast so that they can at least get through more requests.
The other way to push more water downstream is to use a bigger/wider hose. This one is interesting because now it is realized that the water tap can open really wide, and the other side of the hose can push out all of that water in the same time that it takes to produce it. Notice how we are now measuring in terms of work-per-unit-time (the opposite of throughput). In software terms, this is handling concurrency or building capacity. Capacity is the measure of how many simultaneously submitted tasks a system can serve. As the analogy suggests, this is a very different beast, and asynchronous programming patterns hold a very important place here since they allow for at least the acceptance of a large number of tasks without getting locked up.
Consider that systems A and B from our example above are still single threaded, but A is now asynchronously programmed so that its single thread is not blocked when calling B. This system can support multiple users from the get-go because not being blocked allows it to take more work. Also, every optimization in terms of increasing speed/decreasing latency now has a much wider impact across all open requests. When only one request could get faster at a time, now the entire set of requests being buffered by system A reap the benefits. We have a much more scalable system now. There is now the problem of too many requests now reaching B all at once – we will get to it later in this article.
Little’s Law
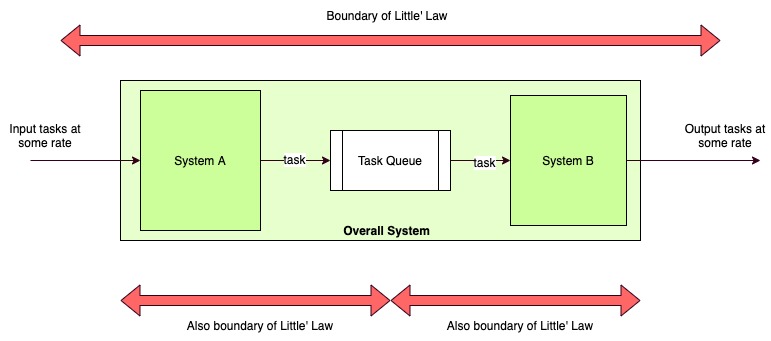
The concepts of throughput and capacity find joint expression in Little’s Law.
At steady state, the average number of items in a queuing system equals the average rate at which items arrive multiplied by the average time that an item spends in the system.
In other words, the amount of water in the hose is a factor of amount-of-water-per-unit-time being pushed in and the time-per-unit-water being removed. In further other words, we cannot define a steady-state system only in terms of throughput, we also need to include its capacity or the amount of unfinished work that can hang around in it.
Why did we add “steady state” there? A system that is already crashing and burning, water hoses exploding or popping out is not very interesting – it is already broken. “Steady state” means that we are trying to describe a system with steady flows and behaviour, aka stable SLAs. If we look at a distributed system like a mesh of water hoses of different sizes connected to each other, we want to be able to tell how much water is flowing where if everything is going well. This is what SLAs are (how fast + how much), and Little’s law allows us to define these elegantly.
By drawing boundaries around any set of connected components, we can monitor their entry/exit rates and volumes and figure out how they will behave under variable load. Yes, I said around “any set of components”. Not only can apply the law around the whole components, we can recursively apply it to sub-sets of components to analyze internal stable states and sum of all these is equal to the superset.
Let’s consider data caching as an optimization strategy. What does it optimize? It reduces the amount of time needed to fulfill a data read request, so we know that we are optimizing for throughput. But have we taken care of all failure patterns now? If we use something like Redis (a single-threaded system), we know that we cannot handle a surge in parallel calls. Now we can go back and perhaps add a read-only slave to our Redis setup, thereby doubling the capacity. Now we are going through requests twice as fast, and the steady-state capacity of our system just went up twofold.
So now that we know all this theory, how do we build a stable, high scale, distributed system?
The only way to build a stable distribute system is to make sure that ALL systems and connections in it are stable. This is where true complexity of microservice architectures emerges – there are system dependencies (often circular), there are fluctuations in the performance of each system, variations in load due to things like traffic or retries-on-failure etc. Beyond a point, it becomes very difficult what will happen when something unexpected happens? The way out is to build communication at each step in such a way that the overall system automatically converges towards stable state due to feedback (positive or negative – usually the latter).
What kind of feedback can we design to achieve this? Theory of Constraints in manufacturing processes has the notion of in-progress-inventory as cost. Once you release some work on a factory floor, it is a liability, eating manpower and materials till it is complete and can be sent out to be sold. If a downstream machine isn’t working, there is no point for workers in upstream processes to be doing a lot of work and generating in-progress-inventory – it will never complete. The factory floor uses this feedback loop to control how much work can be taken at any time. We can apply the same concept to the software system pipeline.
In general, we always want to have “some” surplus capacity (so that we can gracefully handle fluctuations in traffic) without incurring a prohibitive cost for it. The simplest way of adding capacity is to add more hardware to it. But this is often not cost-effective at scale. As we have seen above, asynchronous programming helps us build elastic capacity (because we have a queue as a buffer between two parts of the system) in face of variable load, and we can turn a lot more of our attention to improving the throughput of individual components instead of constantly worrying about capacity of the system.
However, elasticity goes only so far. Accepting more requests than we can handle is always a bad idea, in software as in life. Let me repeat – if our system is a mesh of pipes, we cannot push through more data than the narrowest point allows. This is a big problem in asynchronous design. The buffer between caller and callee is essential for asynchrony, but the same buffer prevents the caller from understanding that the callee is being overwhelmed by the workload being sent it’s way. In the synchronous model, the calling system would start seeing thread-blocking, etc, but asynchronous systems don’t have this feature(bug??). We can set timeouts on the submitted tasks to start shedding load, but this means that we will keep on taking requests only to fail them later (leading to a bad user experience). Circuit breakers can help here, but is there is a more elegant way to achieve flow-balancing dynamically?
Backpressure
Back-pressure is a mechanism to resist the flow of data through software systems so as to maintain a stable flow in face of local variations in capacity and throughput. We want to regulate the flow of water by not letting too much water enter at too much speed, thereby risking the water-hose mesh. To do this, let’s flip the analogy and try to pull data through the system rather than trying to push it.
Let’s say that conceptually, the queue lies inside the producer of the task pipeline, and it is finite in size (NEVER EVER USE INFINITE BUFFERS. EVER. NEVER.). The caller reaches out to the callee, in this case, to get a new task from the buffer to process. The throughput is thus explicitly controlled by the consuming side (which makes sense, he who has to do the work should decide how fast he can go), and the capacity (a measure of open requests) is determined by the calling side by deciding how many unprocessed tasks we want to keep, aka the queue size. If the queue is full because the consumer is not running fast enough, the caller has a choice – he can drop the oldest (and presumably the least relevant) tasks from the queue to make room, or stop taking any more requests immediately (since they will likely fail anyway). This is different from setting task timeouts because we are not saying how long a task should take, but how unfinished tasks the system as a whole can have and still hope to complete them within the SLA.
We can also make the callee own the queue, and let him own both the rate as well as the number of outstanding requests. This centralizes the logic to some extent but it is possible that this system gets so loaded during a traffic surge that it cannot even make the decision of load-shedding.
There are three ways to achieve backpressure:
- Tell the caller to stop giving new tasks: This is usually the best and the most effective way. If a downstream system under load can proactively request a breather, a dynamic equilibrium between producer and consumer can be achieved very quickly. RxJava uses this paradigm.
- Block the caller when he tries to give a new task: This is slightly different because here the caller faces an error situation on producing a new task and he has to take an independent decision on how to handle this error after having taken on the task. Patterns like rate limiting fit in here.
- Start dropping some tasks: Depending on the context, the callee can start dropping the oldest or the newest tasks from the pipeline. This silent behaviour is not my favourite because it gives less visibility into the system unless the caller is monitoring task completion properly, but this is the same thing that gives it value – the callee can independently implement this if the caller cannot be influenced to change behaviour.
Conclusion
This was a lot of heavy stuff! Let’s tl;dr it.
- Distributed systems and asynchronous systems both behave very similarly and can be understood as computational pipelines.
- Throughput is the rate of doing things in the system
- Capacity is the number of tasks that can remain open in the system without breaching the SLA.
- SLA is a joint promise of throughput and capacity given by the downstream system to the upstream system.
- Back-pressure is a mechanism of propagating the knowledge of downstream failures/problems.
- Scaling and stabilizing a system is a constant back-and-forth between addressing throughput issues and capacity issues.
Try this – Go back to a bird’s eye view of your architecture and imagine that all IO-bound processes are asynchronous. What would now be the bottlenecks? Have you explicitly identified fallback behaviours for their callers? What would happen if these fail? And so on and so on. What I expect you will see from this exercise is a combination of throughput and capacity bottlenecks each feeding into each other – and now that you are armed with Little’s Law and back-pressure, you will be able to eliminate them to get to a stable, beautiful system.
Read Next: More article on domain-driven design



One thought on “Distributed Systems as Data Pipelines : Throughput, Capacity, and BackPressure”